Lo que no te contaron de los puentes térmicos: 3 paradojas en la edificación

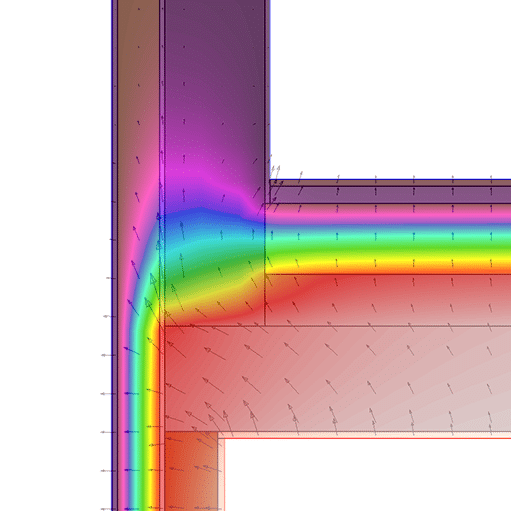
En el análisis energético de este proyecto que hemos realizado hemos encontrado 3 casos que son muy interesantes. Os los explicaremos en este post.

Aislar no siempre es «poner una manta y listo». A veces, la física de edificios nos juega pasadas curiosas donde la geometría y los materiales desafían la lógica común. En la mayoría de los programas —desde los métodos de cálculo simplificados basados en la UNE-EN ISO 52016-1 (como CE3X o CERMA) hasta los más avanzados de cálculo dinámico (EnergyPlus)— se simplifican los modelos reduciendo la envolvente a componentes unidimensionales. Esto permite un cálculo rápido y ajustado, pero perdemos datos relevantes del flujo de calor real.

Por eso, la introducción de los puentes térmicos debe entenderse más como un ajuste del modelo térmico (para introducir particularidades geométricas y constructivas) que como una realidad en términos absolutos. No se puede comparar el puente térmico de una solución constructiva con otra de forma aislada; depende de su contexto.

La paradoja: Aislamos la fachada por el exterior (SATE) y también el retorno hacia el marco de la ventana, pero el valor del puente térmico ($\psi$) aumenta.

• ¿Por qué sucede? Al aplicar un «súper aislamiento» en fachada y cambiar a una ventana de altas prestaciones, la resistencia térmica del conjunto aumenta drásticamente. Si el retorno del aislante en el hueco no es igual de potente o la ventana no está alineada con el aislante, el calor «se concentra» ahí.
• El matiz del modelo: Rigurosamente, no es que el calor «busque» la salida, sino que, en comparación con la fachada mejorada, ese punto es ahora mucho más débil. Como el modelo unidimensional no había previsto esa debilidad, el coeficiente $\psi$ sube para compensarlo.
• La ironía: Si dejásemos la fachada sin aislar (con una transmitancia mala), el puente térmico de ese mismo retorno parecería «mejor» en el cálculo. Por eso, el $\psi$ no es un valor absoluto, sino relativo a lo que tiene al lado.
• Conclusión: La posición de la carpintería respecto al aislante es crítica para evitar que el flujo de calor se concentre.

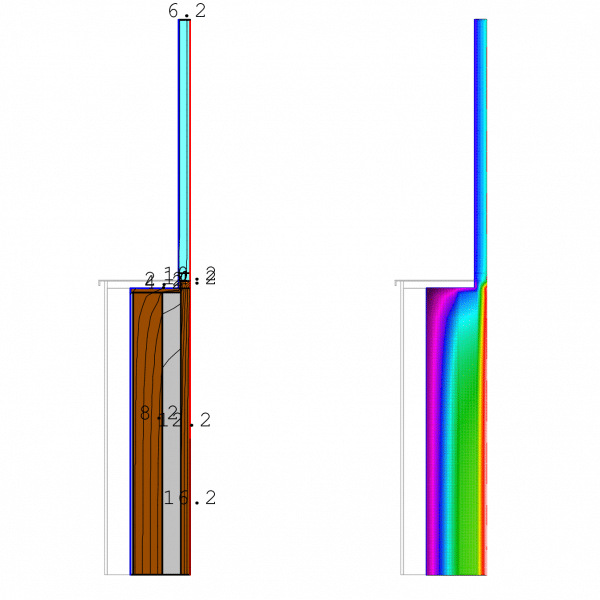
Caso 1.1. El estado inicial: cuando todavia no hemos sustituido carpinteria ni aislado con SATE. La ψ: Transmitancia Puente térmico = 0,11 W/mK

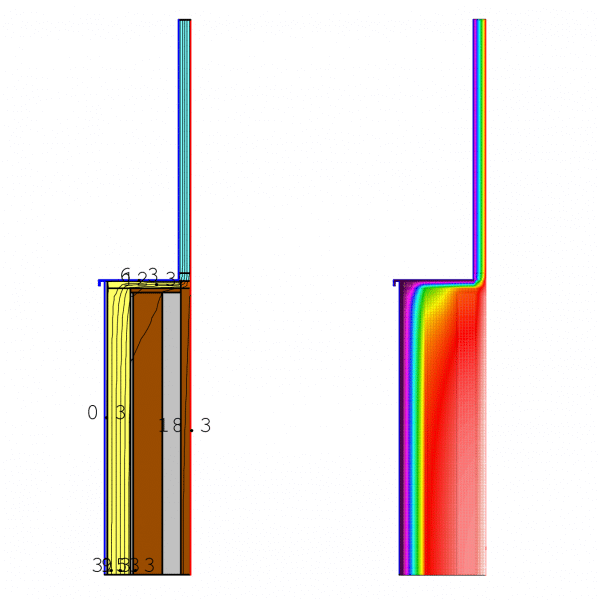
Caso 1.2. Aislamos con 12 cm de SATE y cambiamos las carpinterias por unas que tienen una Uw de menos de 1,40 W/m2k (super aislantes!). El contorno de hueco (jambas y alfeizar se protege con 4 cm de EPS) La ψ: Transmitancia Puente térmico = 0,13 W/mK.

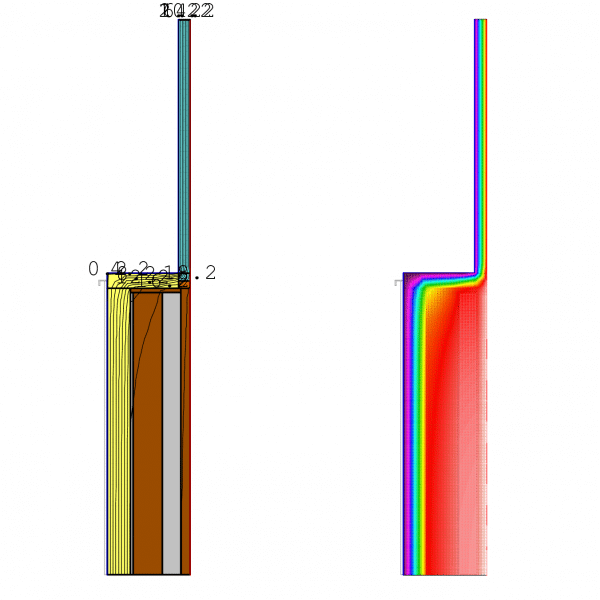
Caso 1.3. Este caso consiste en mejorar el Caso 2 con un retorno de 8 cm de EPS en alfeizar y jambas. Como vemos mejora sustancialmente el puente térmico, no obstante por causas constructivas el grosor del retorno no siempre es posible hacerlo tan grueso. La ψ: Transmitancia Puente térmico = 0,03 W/mK

• La paradoja: En las esquinas interiores (entrantes, es decir cuando el exterior está en una «concavidad»), el coeficiente ψ suele ser negativo. ¿Significa que la esquina genera calor? No, ojalá.
  • ¿Por qué sucede? Es una cuestión de pura geometría y de cómo medimos. Normalmente, en el cálculo de certificados (como CE3X), usamos dimensiones exteriores.
  • La explicación: En una esquina entrante, la superficie exterior es mucho más pequeña que la superficie interior. Al calcular las pérdidas totales usando el área exterior, las fórmulas estándar sobrestiman cuánta energía se está escapando.
  • El ajuste: Para corregir ese exceso de cálculo y que el balance cuadre con la realidad, el valor $\psi$ debe ser negativo. Es un factor de corrección matemática para no castigar injustamente la eficiencia del muro.

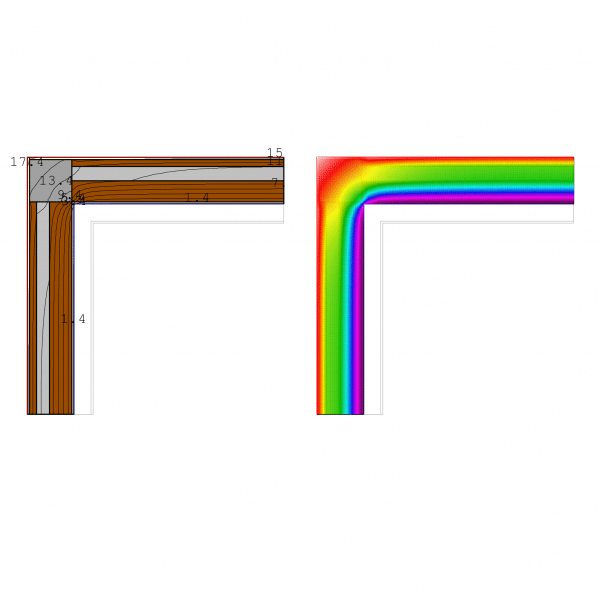
Caso 2.1. Es el estado inicial. Sin la protección de SATE en el conocido puente térmico de «pilar en esquina». La ψ: Transmitancia Puente térmico = -0,55W/mK

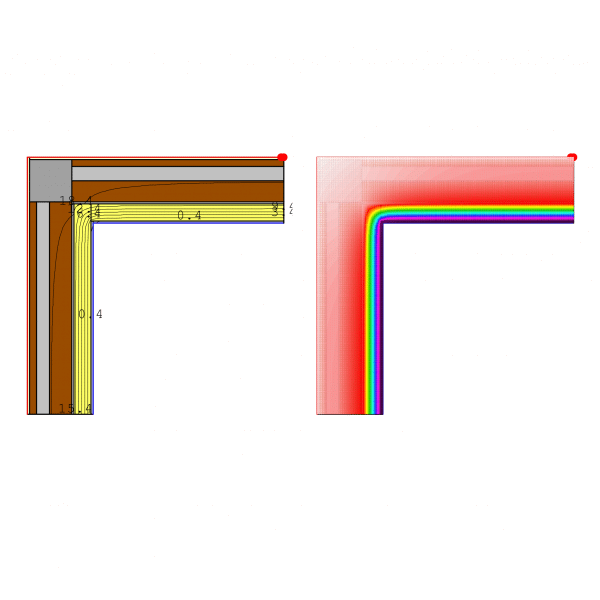
Caso 2.2. Aislamos con SATE. La ψ: Transmitancia Puente térmico = -0,17 W/mK

• La paradoja: Un antepecho de hormigón celular sin una sola placa de aislante puede ser térmicamente más eficiente que un antepecho de hormigón armado envuelto en 10 cm de aislamiento.

  • El concepto clave: El «atajo» del calor. En un antepecho convencional de bloque o hormigón armado, para evitar el puente térmico, nos vemos obligados a «envolver» todo el murete. Esto genera una superficie de intercambio enorme: el calor tiene una «autopista» por el hormigón y una gran superficie de salida a través del aislante.
  • La ventaja del hormigón celular: Al sustituir el bloque por hormigón celular (que tiene una conductividad mucho menor que el armado, aunque peor que un aislante puro), eliminamos la necesidad de envolverlo.
  • El balance final: El flujo de calor se limita estrictamente a la sección del muro. Aunque el material resiste menos que la lana de roca o el EPS, la superficie y longitud de exposición son tan pequeñas comparadas con la «envolvente completa» del caso tradicional, que las pérdidas totales son menores.
  • Menos es más: Una superficie de pérdida reducida compensa con creces una conductividad ligeramente superior.

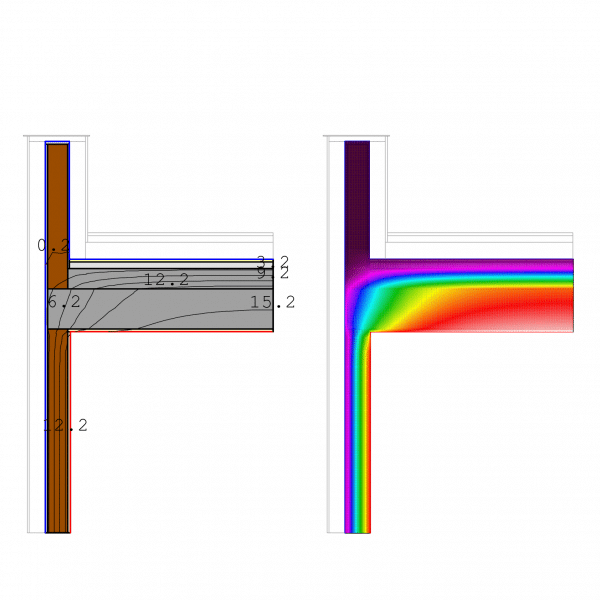
Caso 3.1. Es el estado inicial con el antepecho de ladrillo perforado Sin la protección de SATE ni el aislamiento en la cubierta. La ψ: Transmitancia Puente térmico = 0,73W/mK

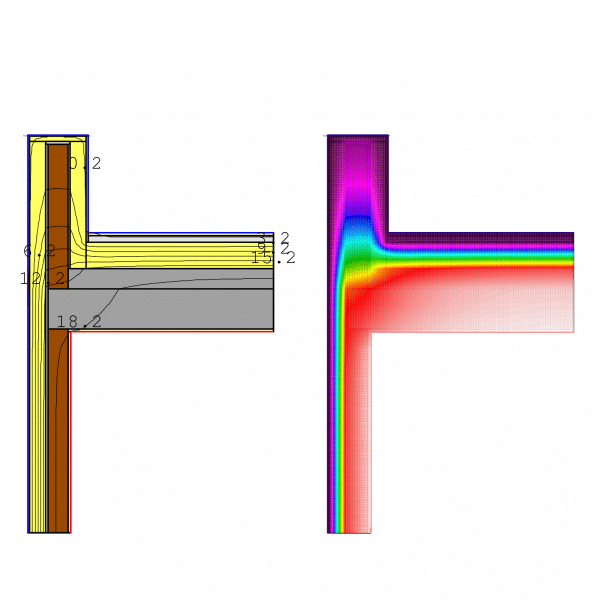
Caso 3.2. Aislamos con 12 cm de EPS en fachada i el antepecho con 4 cm, la cubierta aislada con XPS 20 cm. Obtenemos una ψ: Transmitancia Puente térmico =0,22 W/mK

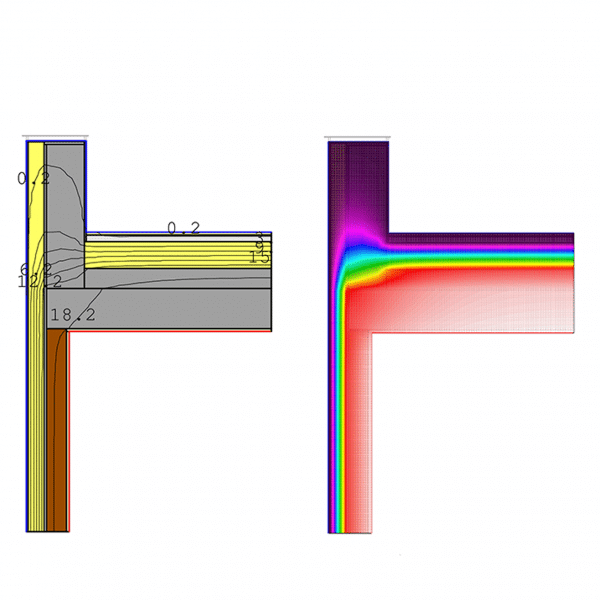
Caso 3.3. Descartamos aislar el antepecho y proponemos un bloque de hormigón celular de 25 cm de ancho y una conductividad de λ  = 0,09, la cubierta aislada con XPS 20 cm. Esto seria mucho más sencillo construcivamente que el caso anterior. Obtenemos una ψ: Transmitancia Puente térmico =0,15W/mK

Los puentes térmicos no son solo «puntos fríos»; son nudos de flujo de energía que delatan la precisión de nuestro modelo. Entender que la geometría (Caso 2) y la resistencia intrínseca de los materiales (Caso 3) mandan sobre la cantidad de aislante (Caso 1) es lo que diferencia a un proyectista de un simple instalador.